一.什么是时间复杂度
网上的公式话很多,这里就不给粘贴过来了,不过我可以给你们推荐一个挺不错的博主,他讲的很浅显易懂的
【帅地大佬的博客 】
总而言之呢,时间复杂度的排序如下:
$$
O(1)<O(log(n))<O(n)<O(nlog(n))<O(n^2)<O(n^3)<O(2n)<O(n!)<O(n^n)
$$
空间复杂度就先不在这里说了哈,网上有很多教程的,遇到空间限制的时候再说
二.排序算法
emm~,我这里会在每种排序下放两种代码,一个python,一个c(要应付考试/(ㄒoㄒ)/~~)
1.冒泡排序
基本思想:通过对待排序序列从前向后(从下标较小的元素开始),依次对相邻两个元素的值进行两两比较,若发现逆序则交换,使值较大的元素逐渐从前移向后部,就如果水底下的气泡一样逐渐向上冒。
没看懂别慌,我有这张神图帮你理解
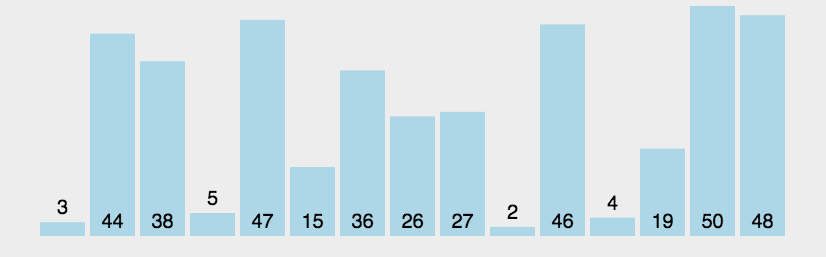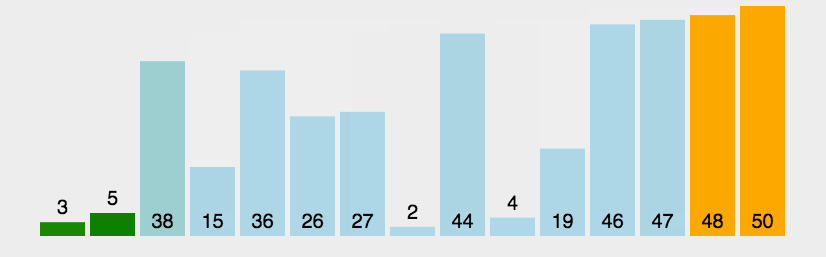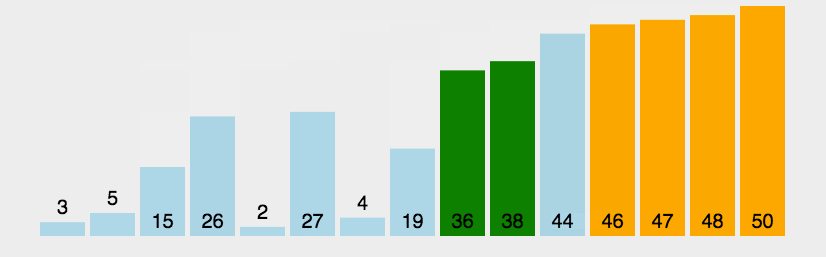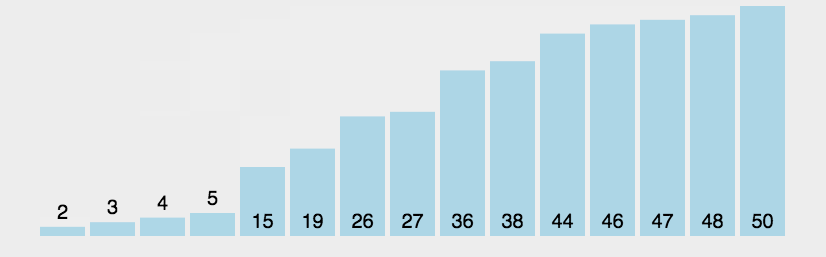
#python代码
def mao_pao(num_list):
num_len=len(num_list)
for j in range(num_len):
sign=False #优化:设置标志位,当循环不再改变顺序时,可以提前跳出循环
for i in range (num_len-1-j):
if a[i]>a[i+1]:
a[i],a[i+1]=a[i+1],a[i]
sign=True
if not sign:
break
if __name__=="__main__":
a=input().split()
mao_pao(a)
print(a)
print(" ".join(a)) #优化:将结果列表中的元素连接成字符串,并在每个元素中加了空格来美化那就让我们审计下最关键的代码
for j in range(num_len):
sign=False #优化:设置标志位,当循环不再改变顺序时,可以提前跳出循环
for i in range (num_len-1-j):
if a[i]>a[i+1]:
a[i],a[i+1]=a[i+1],a[i]
sign=True
if not sign:
break这是排序的关键,外循环控制了循环次数,理论上有多少元素会循环几次
在内循环中,每次比较后,将较大值放在右边,一直重复,直至标志位不再改变后,才能跳出循环
我们看看它的时间复杂度,可以将它分为两种情况
- 如果我们的顺序为正序,那么这就是最理想的情况,走一遍就ok了,所需的比较次数C和记录移动次数M均达到最小值,即Cmin=n-1;Mmin=0,此时它的时间复杂度就为O(n)了
- 如果我们的顺序是反序,那么这就是最坏的情况,共需要n-1遍排序(已经用标志位优化的前提下)。每趟排序要进行n-i-1次比较(1<=i<=n-1)。在这种情况下,比较和移动次数均达到最大值:$$
(n-1)(n-i-1)=O(n^2)
$$
#include <stdio.h>
#define SIZE 100000 /*给数组给个范围,多大都没限制,大点好一点*/
void bubbleSort(int arr[], int n) {
int i, j;
//控制排序的次数
for (i = 0; i < n - 1; i++) {
//每次将最大的放在右边
for (j = 0; j < n - i - 1; j++) {
if (arr[j] > arr[j + 1]) {
// 交换元素
int temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
}
}
}
}
int main() {
int n;
printf("请输入要排序的元素个数:");
scanf_s("%d", &n);
int arr[SIZE];
printf("请输入 %d 个整数:\n", n);
for (int i = 0; i < n; i++) {
scanf_s("%d", &arr[i]);
}
bubbleSort(arr, n);
printf("排序后的结果为:\n");
for (int i = 0; i < n; i++) {
printf("%d ", arr[i]);
}
printf("\n");
return 0;
}
悄悄说一句,c是真的不喜欢/(ㄒoㄒ)/~~
2.选择排序
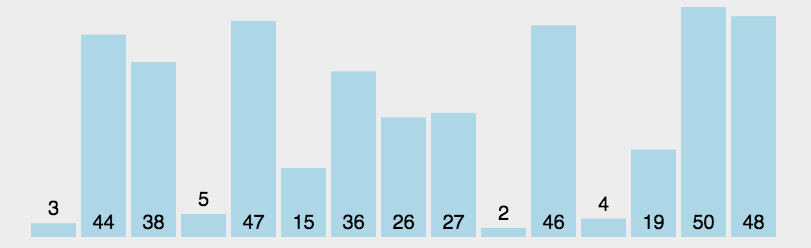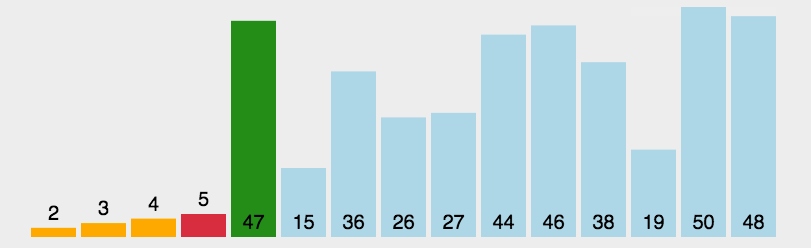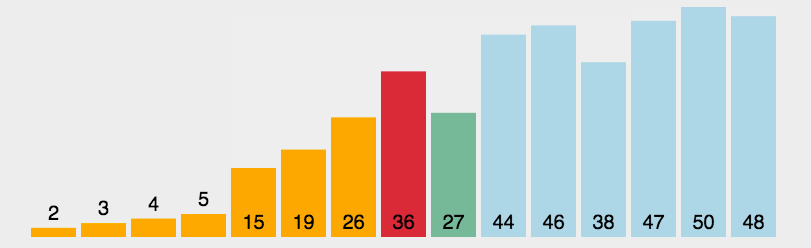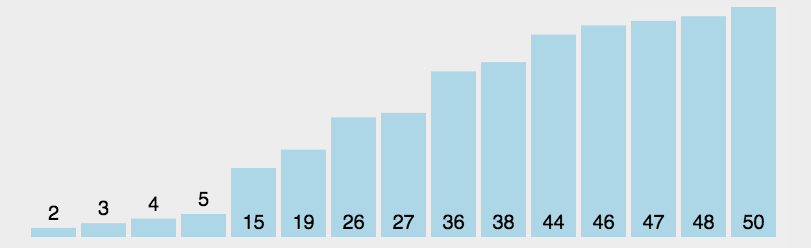
基本思想:选择排序(Selection-sort)是一种简单直观的排序算法。它的工作原理:首先在未排序序列中找到最小(大)元素,存放到排序序列的起始位置,然后,再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾。以此类推,直到所有元素均排序完毕。
简单的说就是每次从剩余元素中选择最小或最大的元素,进行依次排序
from typing import List
def selection_sort(arr: List[int]):
length = len(arr)
if length <= 1:
return
for i in range(length):
min_index = i #标记了排序时第一个数字的下标
min_val = arr[i] #标记了排序时第一个数字
for j in range(i, length):
if arr[j] < min_val:
min_val = arr[j]
min_index = j #看上去有点长,实际上就是干了一件事,找到比min_val还小的数
arr[i], arr[min_index] = arr[min_index], arr[i]
if __name__ == '__main__':
s=input().split()
s=list(map(int,s))
selection_sort(s)
print("选择排序结果:", s)选择排序的比较次数与序列的初始排序无关。假设待排序的系列有n个元素,那么比较次数总是
$$
n(n-1)/2
$$
而移动次数与初始排序状态有关,当初始为顺序时,移动次数最少为0。当初始为逆序时,移动次数最多为
$$
3n(n-1)/2
$$
综上所述,选择排序的时间复杂度是
$$
O(n^2)
$$
#include<stdio.h>
#define SIZE 2000//这是我随便弄的一个范围
void selectSort(int data[], int n)
{
/*----begin------*/
if (n == 1) {
printf("不用排序:%d", data[0]);
}
else {
int i, j;
int min = 0;
for (i = 0; i < n - 1; i++)
{
min = i;
for (j = i + 1; j < n; j++)
{
if (data[min] > data[j])
{
min = j;
}
}
int temp = data[min];
data[min] = data[i];
data[i] = temp;
}
for (i = 0; i < n; i++)
{
printf("%d ", data[i]);
}
}
/*-----end------*/
}
int main() {
int n;
int arr[SIZE];
printf("请输入要排序的元素个数:");
do {
scanf_s("%d", &n);
printf("请输入 %d 个整数:\n", n);
for (int i = 0; i < n; i++) {
scanf_s("%d", &arr[i]);
}
} while (n <= 0 || n > 2000);
selectSort(arr, n);
return 0;
}3.插入排序
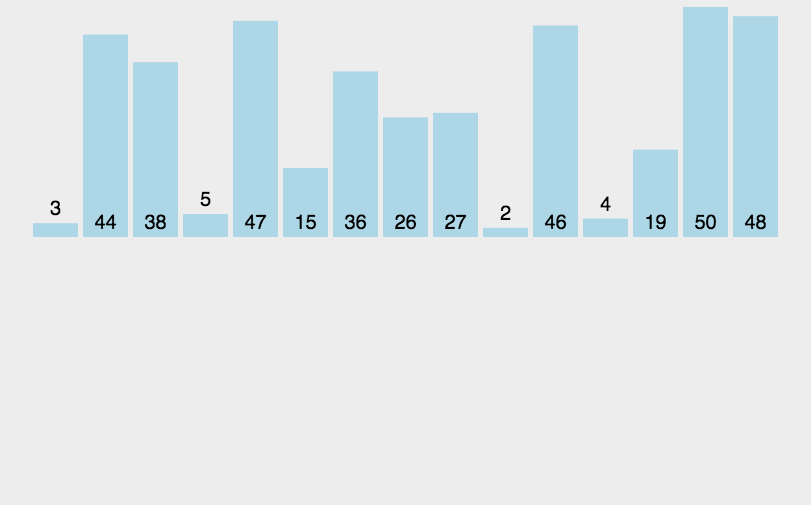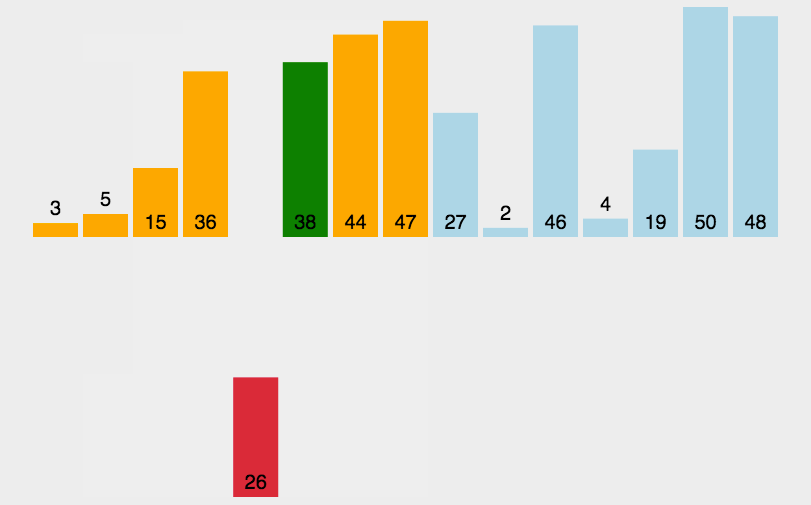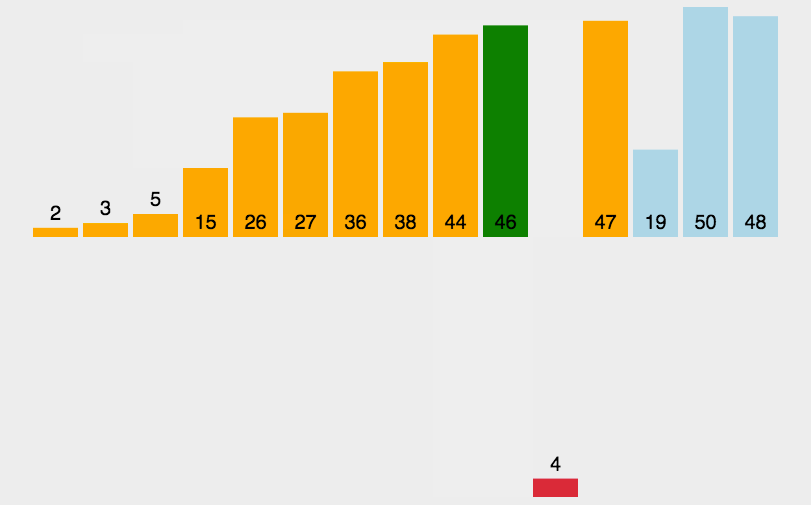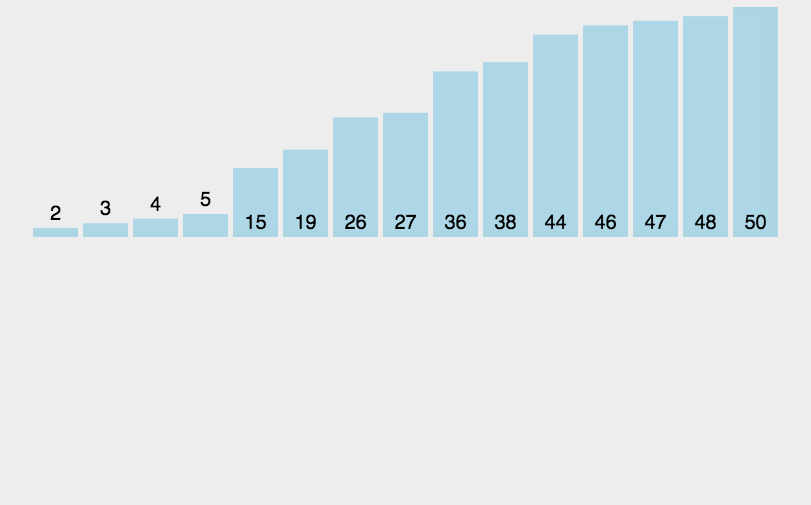
插入排序(Insertion-Sort)的算法描述是一种简单直观的排序算法。它的工作原理是通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。
具体算法描述如下:
- 从第一个元素开始,该元素可以认为已经被排序;
- 取出下一个元素,在已经排序的元素序列中从后向前扫描;
- 如果该元素(已排序)大于新元素,将该元素移到下一位置;
- 重复步骤3,直到找到已排序的元素小于或者等于新元素的位置;
- 将新元素插入到该位置后;
- 重复步骤2~5。
from typing import List
def insertion_sort(arr: List[int]):
length = len(arr)#获取列表长度
if length <= 1:
return
for i in range(1, length):#从第二个元素开始遍历
value = arr[i]
j = i - 1
while j >= 0 and arr[j] > value:
arr[j + 1] = arr[j]
j -= 1
arr[j + 1] = value
if __name__ == '__main__':
s=input("请输入要排序的数字").split()
s=list(map(int,s))
print("原始数据:", s)
insertion_sort(s)
print("插入排序结果:", s) #include <stdio.h>
#define SIZE 2000
// 插入排序函数
void insertion_sort(int arr[], int n) {
int i, j, key;
for (i = 1; i < n; i++) {
key = arr[i];
j = i - 1;
// 将大于 key 的元素向后移动
while (j >= 0 && arr[j] > key) {
arr[j + 1] = arr[j];
j--;
}
arr[j + 1] = key;
}
}
int main() {
int arr[SIZE];
int elements;
printf("请输入元素个数:");
do {
scanf_s("%d", &elements);
printf("请输入这%d个整数:", elements);
for (int i = 0; i < elements; i++) {
scanf_s("%d", &arr[i]);
}
} while (elements <= 0 || elements > 2000);
//int n = sizeof(arr) / sizeof(arr[0]); 相当于py里的len()
printf("原始数据:");
for (int i = 0; i < elements; i++) {
printf("%d ", arr[i]);
}
printf("\n");
insertion_sort(arr, elements);
printf("插入排序结果:");
for (int i = 0; i < elements; i++) {
printf("%d ", arr[i]);
}
printf("\n");
return 0;
}
4.希尔排序
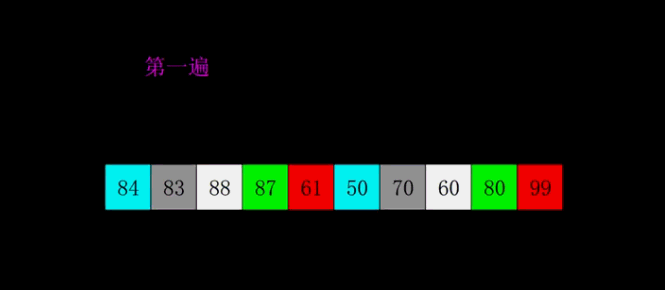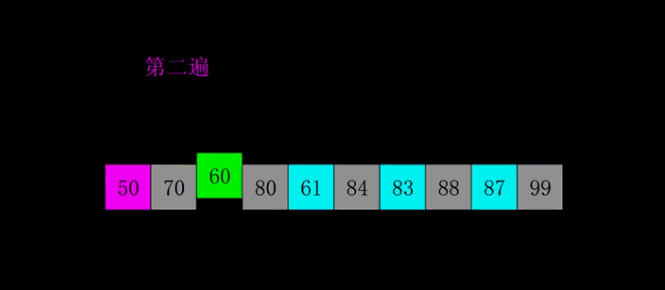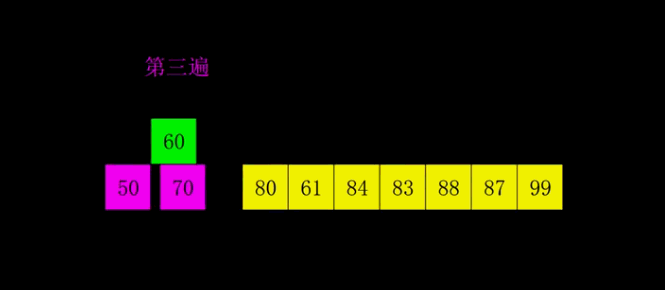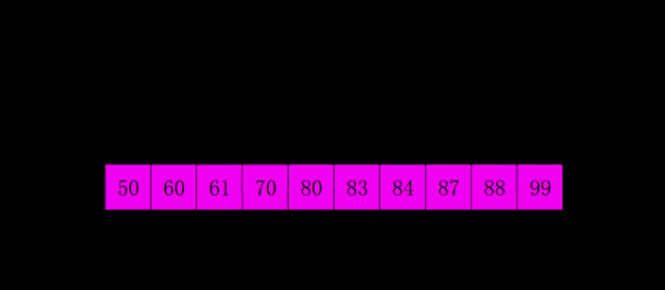
希尔排序的核心在于间隔序列的设定。既可以提前设定好间隔序列,也可以动态的定义间隔序列。
具体过程:
- 先将整个待排序的记录序列分割成为若干子序列分别进行直接插入排序
- 选择一个增量序列t1,t2,…,tk,其中ti>tj,tk=1
- 按增量序列个数k,对序列进行k 趟排序
- 每趟排序,根据对应的增量ti,将待排序列分割成若干长度为m 的子序列,分别对各子表进行直接插入排序。仅增量因子为1 时,整个序列作为一个表来处理,表长度即为整个序列的长度
def shell_sort(array):
n = len(array)
gap = n // 2
while gap > 0:
for i in range(gap, n):
for j in range(i, gap-1, -gap):
if array[j] < array[j-gap]:
array[j], array[j-gap] = array[j-gap], array[j]
else:
break
gap //= 2
return array
if __name__ == '__main__':
s=input("请输入要排序的数字").split()
s=list(map(int,s))
print("原始数据:", s)
shell_sort(s)
print("插入排序结果:", s) #include <stdio.h>
#define SIZE 2000
// 希尔排序函数
void shell_sort(int arr[], int n) {
int gap, i, j, temp;
for (gap = n / 2; gap > 0; gap /= 2) {
for (i = gap; i < n; i++) {
temp = arr[i];
for (j = i; j >= gap && arr[j - gap] > temp; j -= gap) {
arr[j] = arr[j - gap];
}
arr[j] = temp;
}
}
}
int main() {
int arr[SIZE];
int elements;
printf("请输入元素个数:");
do {
scanf_s("%d", &elements);
printf("请输入这%d个整数:", elements);
for (int i = 0; i < elements; i++) {
scanf_s("%d", &arr[i]);
}
} while (elements <= 0 || elements > 2000);
printf("原始数据:");
for (int i = 0; i < elements; i++) {
printf("%d ", arr[i]);
}
printf("\n");
shell_sort(arr, elements);
printf("希尔排序结果:");
for (int i = 0; i < elements; i++) {
printf("%d ", arr[i]);
}
printf("\n");
return 0;
}
5.归并排序
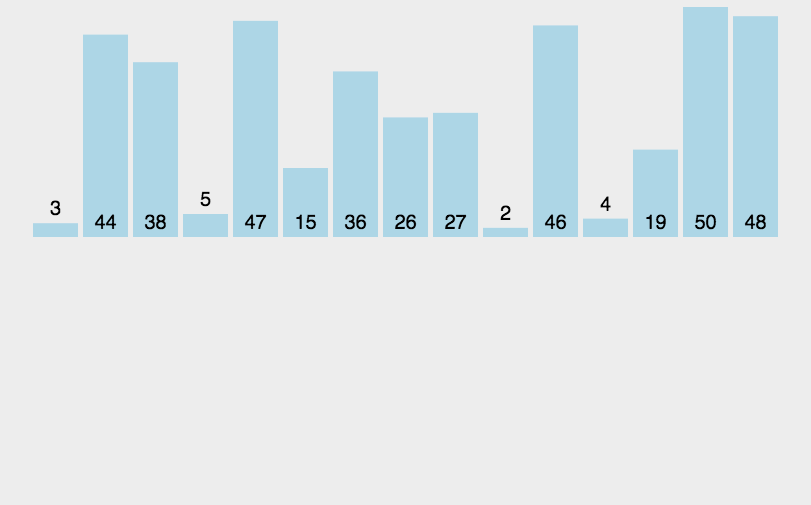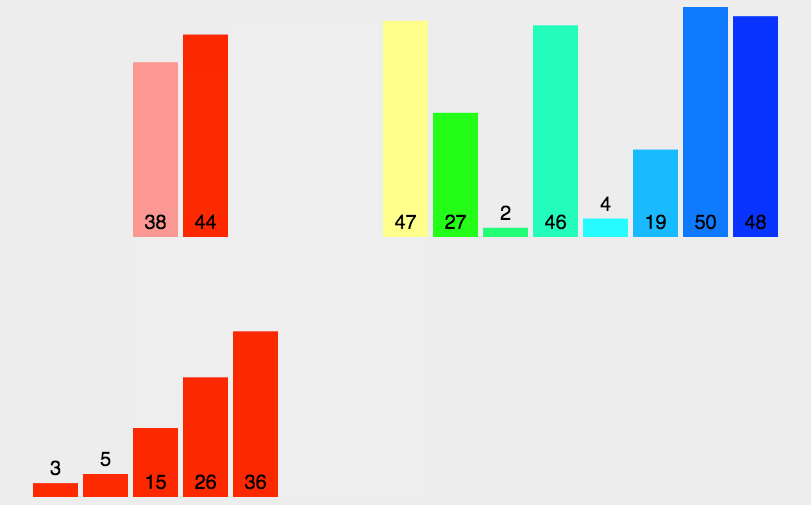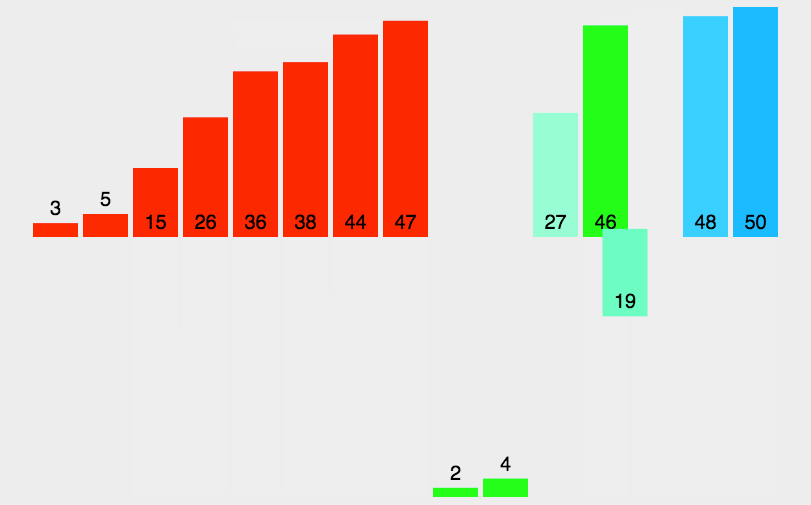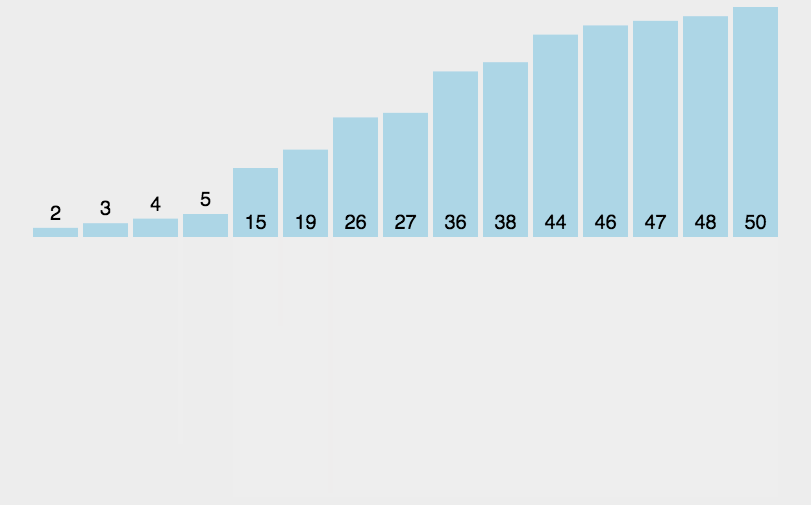
归并排序的核心原理是采用分治法(Divide and Conquer),递归调用;将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。然后将两个有序表合并成一个有序表,最终完成所有元素的排序。
def merge(left, right):
# 合并两个有序列表
res = []
while len(left) > 0 and len(right) > 0:
if left[0] < right[0]:
res.append(left.pop(0))
else:
res.append(right.pop(0))
if left:
res.extend(left)
if right:
res.extend(right)
return res
def mergeSort(arr):
# 归并函数
n = len(arr)
if n < 2:
return arr
middle = n // 2
left = arr[:middle] # 取序列左边部分
right = arr[middle:]# 取序列右边部分
# 对左边部分序列递归调用归并函数
left_sort = mergeSort(left)
# 对右边部分序列递归调用归并函数
right_sort = mergeSort(right)
#
return merge(left_sort, right_sort)
if __name__ == '__main__':
s=input("请输入要排序的数字").split()
s=list(map(int,s))
print("原始数据:", s)
s=mergeSort(s) #这里记得赋值,函数里面是重新定义了列表,需要我们更新下数据
print("归并排序结果:", s) #include <stdio.h>
#define SIZE 2000
// 合并两个有序数组
void merge(int arr[], int left, int middle, int right) {
int i, j, k;
int n1 = middle - left + 1;
int n2 = right - middle;
// 创建临时数组
int L[SIZE], R[SIZE];
// 将数据复制到临时数组
for (i = 0; i < n1; i++)
L[i] = arr[left + i];
for (j = 0; j < n2; j++)
R[j] = arr[middle + 1 + j];
// 合并临时数组
i = 0;
j = 0;
k = left;
while (i < n1 && j < n2) {
if (L[i] <= R[j]) {
arr[k] = L[i];
i++;
}
else {
arr[k] = R[j];
j++;
}
k++;
}
// 复制剩余元素
while (i < n1) {
arr[k] = L[i];
i++;
k++;
}
while (j < n2) {
arr[k] = R[j];
j++;
k++;
}
}
// 归并排序
void mergeSort(int arr[], int left, int right) {
if (left < right) {
int middle = left + (right - left) / 2;
// 对左边部分递归排序
mergeSort(arr, left, middle);
// 对右边部分递归排序
mergeSort(arr, middle + 1, right);
// 合并排序后的左右部分
merge(arr, left, middle, right);
}
}
int main() {
int arr[SIZE];
int elements;
printf("请输入元素个数:");
do {
scanf_s("%d", &elements);
printf("请输入这%d个整数:", elements);
for (int i = 0; i < elements; i++) {
scanf_s("%d", &arr[i]);
}
} while (elements <= 0 || elements > 2000);
printf("原始数据:");
for (int i = 0; i < elements; i++) {
printf("%d ", arr[i]);
}
printf("\n");
mergeSort(arr, 0, elements - 1);
printf("归并排序结果:");
for (int i = 0; i < elements; i++) {
printf("%d ", arr[i]);
}
printf("\n");
return 0;
}
6.快速排序
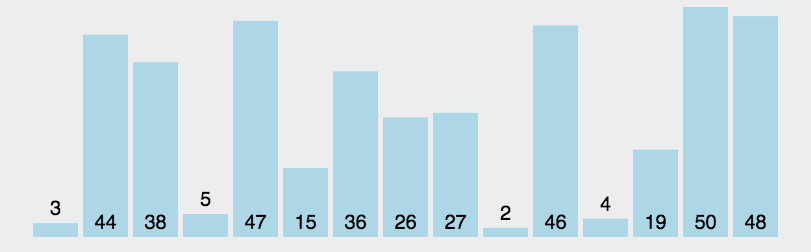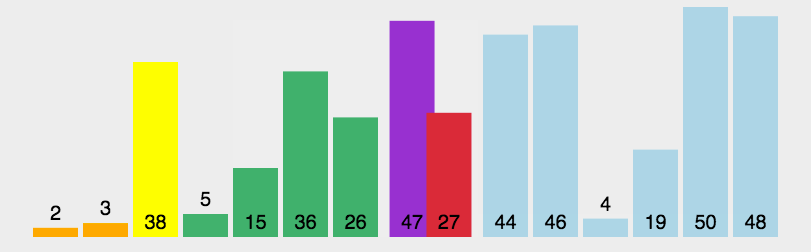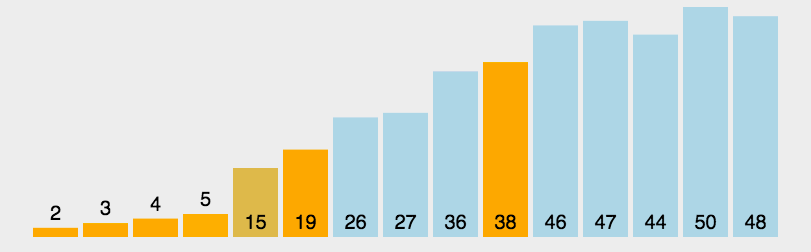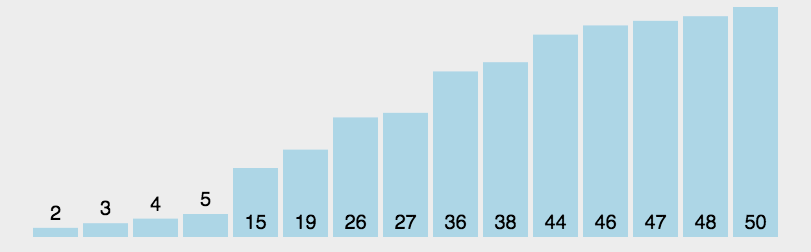
快速排序的基本思想:通过选择一个关键字,一趟排序将待排记录分隔成独立的两部分,其中一部分数据均比选取的关键字小,而另一部分数据均比关键字大,则可分别对这两部分记录继续进行排序,以达到整个序列有序。快速排序使用分治法(Divide and conquer)策略来把一个序列(list)分为较小和较大的2个子序列,然后递归地排序两个子序列。
过程描述:快速排序使用分治法来把一个串(list)分为两个子串(sub-lists)。
- 从数列中挑出一个元素,称为
“基准”(pivot); - 重新排序数列,所有元素比基准值小的摆放在基准前面,所有元素比基准值大的摆在基准的后面(相同的数可以到任一边)。在这个分区退出之后,该基准就处于数列的中间位置。这个称为
分区(partition)操作; - 递归排序子序列:
递归地(recursive)把小于基准值元素的子数列和大于基准值元素的子数列排序。
# 左小右大函数,获取一个中值,左放小右放大函数
def partition(arr, low, high): #参数:列表,列表的第一个索引0,最后一个索引值N
i = low # 最小元素索引
pivot = arr[high] # 最后一个元素,我们把列表中的所有元素同它比较
for j in range(low, high): #从第一个索引到倒数第二个索引
if arr[j] <= pivot: #从第一个元素到倒数第二个元素依次判断是否≤最后一个元素
arr[i], arr[j] = arr[j], arr[i] #≤最后一个元素的所有元素依次放在左边索引0~i的位置
i = i + 1
arr[i], arr[high] = arr[high], arr[i] #然后将最后一个元素放在索引i的位置,实现:该元素左边的都比它小,右边的都比它大的排序
return (i) #返回该元素的索引位置
# 快速排序函数
def quickSort(arr, low, high):
if low < high: #如果列表有1个以上的元素
pi = partition(arr, low, high) #获取左小右大函数中的 被比较数所在的索引
quickSort(arr, low, pi - 1) #反复循环,左排序
quickSort(arr, pi + 1, high) #反复循环,右排序
arr = input("请输入要排序的数字").split()
arr=list(map(int,arr))
low = 0
high = len(arr)-1
quickSort(arr, low, high)
print(arr)#include <stdio.h>
#include <stdlib.h>
#define SIZE 2000
int compare(const void* a, const void* b) {
return (*(int*)a - *(int*)b);
}
int main() {
int arr[SIZE];
int elements;
printf("请输入元素个数:");
do {
scanf_s("%d", &elements);
printf("请输入这%d个整数:", elements);
for (int i = 0; i < elements; i++) {
scanf_s("%d", &arr[i]);
}
} while (elements <= 0 || elements > 2000);
printf("原始数据:");
for (int i = 0; i < elements; i++) {
printf("%d ", arr[i]);
}
printf("\n");
qsort(arr, elements, sizeof(int), compare);
printf("Sorted array: ");
for (int i = 0; i < elements; i++) {
printf("%d ", arr[i]);
}
return 0;
}
7.堆排序
8.计数排序
9.桶排序
10.基数排序
太难了,等我再学学,然后放上面去





Comments 1 条评论
测试一下下
